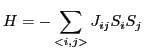Computing Exact Ground States of Ising Spin Glasses
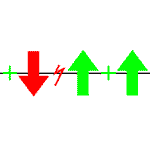
A spin-glass instance in the Ising model is given by n spins that can
either point up or down. Spin i and j are
coupled with coupling strength Jij. We mainly
consider systems in which spins are
located on the sites of a d-dimensional
lattice with nearest neighbor interactions.
The Hamiltonian energy function H is given by
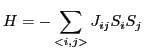where the sum runs over all coupled spins. For a spin i pointing up, its spin variable Si takes value
Si=1,
otherwise Si=-1. A ground state is a spin
configuration that attains the global minimum
of the energy function H. In contrast to
heuristic algorithms used by many physicists,
we determine provably exact ground states. Calculating
an exact ground state of a spin glass in the
Ising model amounts to determining a maximum
cut in the associated graph of
interactions. The algorithm has been
developed at the Computer Science Department in
Cologne in collaboration with several other
researchers. It is quite effective in practice and makes it possible
to gain further insight into the ruling physics of the systems.
